Read other articles:

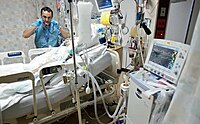
Ventilasi buatan Ventilasi buatan adalah cara membantu atau menstimulasi respirasi proses metabolisme yang mengacu pada pertukaran keseluruhan gas dalam tubuh dengan ventilasi paru, respirasi eksternal, dan respirasi internal.[1][2] Ini dapat berupa pemberian udara secara manual untuk seseorang yang tidak bernapas atau tidak melakukan upaya pernapasan yang memadai, atau ventilasi mekanis yang melibatkan penggunaan ventilator mekanik untuk memindahkan udara masuk dan keluar par...

Kementerian Jal ShaktiLambang IndiaInformasi lembagaDibentukMei 2019[1]Wilayah hukumRepublik IndiaMenteriGajendra Singh Shekhawat, Menteri KabinetPrahlad Singh Patel, Menteri NegaraBishweswar Tudu, Menteri NegaraSitus webwww.mowr.gov.in Kementerian Jal Shakti (terj. har. 'tenaga/pemanfaatan air') adalah sebuah kementerian di bawah pemerintahan India yang dibentuk pada Mei 2019 di bawah kementerian Modi kedua. Kementerian tersebut dibentuk dengan pengggabungan dua kementerian...

Dewan Perwakilan Rakyat Kota Sabang DPRK Sabang2019-2024JenisJenisUnikameral Jangka waktu5 tahunSejarahSesi baru dimulai2 September 2019PimpinanKetuaMuhammad Nasir (Partai Aceh) sejak 21 Oktober 2019 Wakil Ketua IArmadi (Demokrat) sejak 21 Oktober 2019 Wakil Ketua IIFerdiansyah (Golkar) sejak 21 Oktober 2019 KomposisiAnggota20Partai & kursi  NasDem (1)   Demokrat (2)   PAN (1)   Golkar (2)   PBB (2)   PKS (1)  &#...

Chronologie de la France ◄◄ 1778 1779 1780 1781 1782 1783 1784 1785 1786 ►► Chronologies Le festin royal. Fêtes données au Roi et à la Reine par la Ville de Paris le 11 janvier 1782 à l’occasion de la naissance de Monseigneur le DauphinDonnées clés 1779 1780 1781  1782  1783 1784 1785Décennies :1750 1760 1770  1780  1790 1800 1810Siècles :XVIe XVIIe  XVIIIe  XIXe XXeMillénaires :-Ier Ier  IIe  IIIe Chronologies géogra...

Kurva bicorn Dalam geometri, bicorn adalah sebuah kurva kuartik rasional yang didefinisikan dengan persamaan[1] y 2 ( a 2 − x 2 ) = ( x 2 + 2 a y − a 2 ) 2 . {\displaystyle y^{2}(a^{2}-x^{2})=(x^{2}+2ay-a^{2})^{2}.} Kurva ini mempunyai dua taring dalam simetrik mengenai sumbu- y {\displaystyle y} .[2] Kurva bicorn dikenal sebagai kurva topi berbentuk segitiga lantaran mempunyai kemiripannya dengan topi bicorne. Sejarah Pada tahun 1864, James Joseph Sylvester memp...

Miss International 2009Tanggal28 November 2009TempatSichuan International Tennis Center, Chengdu, Sichuan, Republik Rakyat TiongkokPembawa acaraLiu Yi Wei, Li AiPenyiaranCDTV-2Peserta65[1]Finalis/Semifinalis15DebutKuba, Gabon, Georgia, Kirgizstan, UgandaTidak tampilGuatemala, Hawaii, Italia, Liberia, Selandia Baru, Republik Kongo, Serbia, Suriname, Sri Lanka, Swedia, Tanzania, Ukraina, ZambiaTampil kembaliHonduras, Martinik, Moldova, Belanda, Nikaragua, Kepulauan Marian...

كأس إسكتلندا 1889–90 تفاصيل الموسم كأس إسكتلندا  البلد المملكة المتحدة  عدد المشاركين 158   كأس إسكتلندا 1888–89  كأس إسكتلندا 1890–91  تعديل مصدري - تعديل   كأس اسكتلندا 1889–90 (بالإنجليزية: 1889–90 Scottish Cup)‏ هو موسم من كأس اسكتلندا. كان عدد الأندية المشاركة فيه  158.[1&...

Синелобый амазон Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:ЗавропсидыКласс:Пт�...

Propagating disturbance Shockwave redirects here. For other uses, see Shockwave (disambiguation). Bombshock redirects here. For the Transformers character, see Micromasters. This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (September 2015) (Learn how and when to remove this template message) Schlieren photograph of an attached shock on a sharp-nosed supersonic ...

Koordinat: 6°53′40″S 109°39′35″E / 6.8945114°S 109.65963°E / -6.8945114; 109.65963 Universitas PekalonganMotoKampus KreatifJenisPerguruan Tinggi SwastaDidirikan1980RektorSuryani, S.H., M.Hum.AlamatJl. Sriwijaya No.3,, Kota Pekalongan, Jawa Tengah - 51119, Indonesia Situs webhttps://unikal.ac.id Universitas Pekalongan (Unikal) adalah perguruan tinggi swasta yang berkedudukan di Kota Pekalongan, Jawa Tengah. Unikal berdiri pada 15 Februari 1980 merupakan prak...

Japanese professional wrestler Shota UminoUmino in November 2023Birth nameShota UminoBorn (1997-04-17) April 17, 1997 (age 27)Tokyo, JapanProfessional wrestling careerRing name(s)Shota Umino[1]Shota Unno[2]Billed height183 cm (6 ft 0 in)[1]Billed weight93 kg (205 lb)[1]Billed fromTokyo, JapanTrained byHiroshi TanahashiHiroyoshi TenzanJon MoxleyJushin Thunder LigerNJPW Dojo[3]Yuji NagataDebutApril 13, 2017[1] Shota U...

Robur-le-Conquérant Frontispice du roman. Auteur Jules Verne Pays France Genre Roman d'anticipation Éditeur Pierre-Jules Hetzel Date de parution 1886 Illustrateur Léon Benett Nombre de pages 318 Chronologie Série Voyages extraordinaires Frritt-Flacc Nord contre Sud modifier  Robur-le-Conquérant est un roman d'anticipation de Jules Verne, paru en 1886. Historique Le roman paraît d'abord en feuilleton dans le Journal des débats politiques et littéraires, du 29 juin au 18 août 188...

本條目存在以下問題，請協助改善本條目或在討論頁針對議題發表看法。 此條目需要編修，以確保文法、用詞、语气、格式、標點等使用恰当。 (2013年8月6日)請按照校對指引，幫助编辑這個條目。（幫助、討論） 此條目剧情、虛構用語或人物介紹过长过细，需清理无关故事主轴的细节、用語和角色介紹。 (2020年10月6日)劇情、用語和人物介紹都只是用於了解故事主軸，輔助�...

Jack Shephard UniversoLost Lingua orig.Inglese AutoriJ. J. Abrams Damon Lindelof Jeffrey Lieber 1ª app. inPilota, prima parte Ultima app. inLa fine Interpretato daMatthew Fox Voce italianaVittorio Guerrieri Caratteristiche immaginarieSessoMaschio Etnia Stati Uniti Luogo di nascitaLos Angeles, California, USA Data di nascita3 Dicembre 1969 Professioneneurochirurgo AffiliazioneSopravvissuti del volo Oceanic 815 (sezione centrale) «Cammina tra di noi, ma non è uno di noi» (Mess...

2018 Utah House of Representatives election ← 2016 November 6, 2018 (2018-11-06) 2020 → All 75 seats in the Utah House of Representatives38 seats needed for a majority   Majority party Minority party   Leader Greg Hughes Brian King Party Republican Democratic Leader since January 26, 2015 January 26, 2015 Leader's seat 51–Draper 28–Salt Lake City Last election 62 seats, 78.7% 13 seats, 21.3% Seats before 62 13 Seats ...

Australian television channel This article is about the Australian television channel. For other uses, see Extra (disambiguation). Television channel ExtraLogo used between 2012 and 2018, then used again since 2020TypeAlternative programmingCountryAustraliaBroadcast areaSydney, Melbourne, Brisbane, Adelaide, Perth, Darwin and Northern NSW & Gold CoastNetworkNine NetworkProgrammingLanguage(s)EnglishPicture format576i (SDTV) 16:9Timeshift serviceExtra 2(2013–2015)OwnershipOwnerNine Entert...

One PieceMusim 2Grand LineGambar sampul DVD volume pertama.Negara asalJepangJml. episode16RilisJaringan asliFuji TelevisionTanggal disiarkan21 Maret (2001-03-21) –19 Agustus 2001 (2001-8-19)Kronologi Musim← SebelumnyaMusim 1 Berikutnya →Musim 3 Musim kedua dari seri anime One Piece disutradarai oleh Kōnosuke Uda dan diproduksi oleh Toei Animation.[1] Musim ini berisi satu arc cerita tunggal, yaitu Gurando Rain Totsunyū (グランドライン突入, ter...

Survivor Series: WarGamesPoster promosi menampilkan Cody RhodesInformasiPromotorWWEMerekRawSmackDownTanggal25 November 2023Kehadiran17,138[1]TempatAllstate ArenaLokasiRosemont, IllinoisKronologi acara WWE Network Crown Jewel Survivor Series: WarGames NXT Deadline Kronologi Survivor Series 2022 Survivor Series: WarGames Survivor Series: WarGames 2023 adalah acara bayar-per-tayang (PPV) gulat profesional Survivor Series tahunan ke-37 dan acara aliran langsung yang diproduksi oleh WWE. A...

Ornamental motif Composite capital with acanthus leaves The acanthus (Ancient Greek: ἄκανθος) is one of the most common plant forms to make foliage ornament and decoration in the architectural tradition emanating from Greece and Rome.[1] Architecture Timeline of acanthus styles: a) Greek; b) Roman; c) Byzantine; d) Romanesque; e & f) Gothic; g) Renaissance; h & i) Baroque; j & k) Rococo Acanthus mollis leaf; in both this and A. spinosus the leaf forms are rather va...

Probabilistic model This article is about the representation of probability distributions using graphs. For the computer graphics journal, see Graphical Models. Part of a series onMachine learningand data mining Paradigms Supervised learning Unsupervised learning Semi-supervised learning Self-supervised learning Reinforcement learning Meta-learning Online learning Batch learning Curriculum learning Rule-based learning Neuro-symbolic AI Neuromorphic engineering Quantum machine learning Problem...